加重平均　重み　英語でweight　ウエイト

加重平均は統計学初級の概念と考えるが、なじみが薄い。しかし　理解して慣れたら、実に便利な概念なのだ。

マンション価格を用いた　加重平均の例題

下の表を見ないで、次の質問を考えてみよう。

今、5階建ての新築マンションが売り出されている。
その平均価格は、1階から5階まで順に
3020,  3070,  3120,  3180,  5080万円である。
このマンションの平均価格はいくらでしょう？

(3020+3070+3120+3180+5080)/5 = 3494 万円と答える。
これは単純な平均法、算術平均とか相加平均と呼ばれる計算方法による結果である。

そこで下の図表を見せて、こう説明をする。
実は、そのマンションは2階から4階までは6戸づつあるが、1階と5階は3戸しかない。
1階は入り口と駐車場でスペースが限られ、また5階は広い部屋を持つ戸が準備されている。

それでは売主の立場に立って、この新築マンションの全戸が売れた場合の総額を計算してみよう。
すると、8億520万円となる。
全戸は24戸だから、平均価格は 3355 万円と計算できる。
先ほどの3494万円とは異なる。
これは　”総額方式による計算法” で、この平均価格 3355 万円が正しい値である。

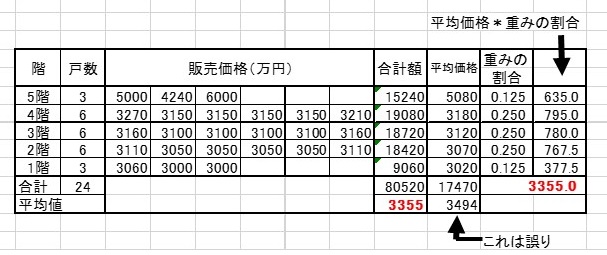
それに対して、各階の平均価格から、全体の平均価格を求める方法を紹介しよう。
ポイントとなるのは、各階に同じ戸数があるのではなく、戸数が違う点にある。
もし各階に同じ戸数がある場合なら、算術平均法を使用することができる。

表の右列に書いた　重みの割合　つまり全戸24戸に対して各階の戸数の割合を　各階の平均価格に乗じてから加算すると
　3355円となり、総額方式で求めた平均価格と同じになる。

このように、各階の平均価格に重みをつけて計算する方法を　加重平均　と呼ぶ。

なお、ここではわかりやすいようにわざわざ　重みの割合　と記したが、 普通、単に重みと言って　重みの割合をさすことの方が多い。 しかしこの場合、戸数を重みと言っても差し支えない。

ウエイト　重み

統計用語としての重みは、英語で weight であり、日本語でもウエイトという人が多い。
私もウエイトの方が好きだから、他のページでもウエイトを使う。

総額方式で考えると、一見 ウエイトの概念が必要無くなるが、実は計算の過程で　“各階の戸数”が　ウエイトとして機能している。
このように重み　ウエイト概念は極めて便利な概念なのだ。
厳密さを求める数学で、これほど曖昧な概念は無いだろう。この原因については機会があったら追加したい。

ウエイト概念は（数学にルーツを持つことを意識することなく）日常生活でも使われている。
受験生があるときに　「これから英語ではなく数学にウエイトを置くつもりだ」というような表現である。
数学勉強に何時間懸けるなどという具体的な数値目標を掲げる必要も無く、また勉強時間の問題ではなく、朝のフレッシュな時間帯に数学勉強をするという心構えを述べただけかもしれない。 そんな”曖昧”性を帯びた数学用語である。

ウエイト概念は数学の別の分野からの導入である。統計学用語として
加重平均法　a weighted meaning method, 加重平均値　weighted mean, weighted average
重み　weight  または　ウエイト

日本語の辞書で紹介されている一般的な用法として
三省堂　 大辞林では　ウエートとして提示され、その②として
重要視して，力を入れること。力点。重点。重要度　　　と記載されている。
ウエイトを置く　ウエイトをかける　ウエイトを載せる　ウェイトを占める　など

この加重平均やウエイトは　2019年初来問題となっている　毎月勤労統計調査の統計学を理解する上で、大変重要な概念です。
興味のある方は　毎月勤労統計調査の統計学のページを参照ください。